このドキュメントは http://edu.net.c.dendai.ac.jp/introduction/algorithm.html から入手できます。
本日の講義内容の要約をA4用紙の表面にまとめなさい。
なお、気が向いたら講義の感想を裏面に書いていただけるとありがたいです。
ネットワークシステム研究室
坂本直志
コンピュータプログラムを作る際に必要な知識とは……
小説を書く場合の、「言葉」と「表現手法」の関係。
今日はこのプログラミング言語の命令の組合せ方について考える。
コンピュータで解決すべき問題があったとしよう。 その時、どのように解決しなければならないかは、どんなプログラミング言語でも 大体同じ。 (書き易さは違っても、書かねばならない内容は同じ) これは、日本語でも英語でも、同じ内容の小説を書く場合、並ぶ単語の意味は大体同じになるのと同様である。
問題の解決の仕方を「アルゴリズム」と呼ぶ。 文章の書き方と同様、アルゴリズムは科学技術が発展しても、変らない。 (たとえ、プログラミング言語は変化していっても)
今日は「アルゴリズム」の話題について紹介する。

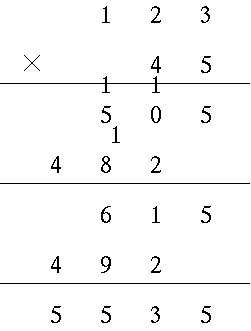
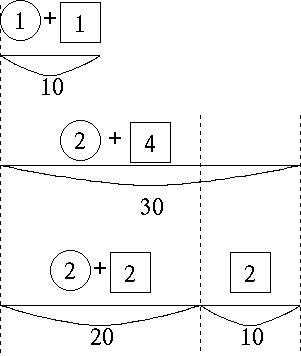
つるとかめが合計で 10 匹。足の数が合計で30 本の時、つる、かめはそれぞれ何匹いるか?
()という方程式の解き方
(, とも実数) の解の判定
を で割る。
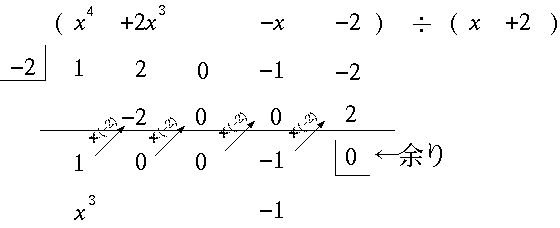
アルゴリズムの良し悪しは、効率に大きく影響する。ここでは、 大きく効率が変わる例を示す。
書物の中から、ある単語の載っているページを知りたい。
1 ページ目から順番に探していく。
1000ページの本だったら、最悪 1000 回探さなければならない。辞書の場合、単語は辞書順に並んでいる。
辞書順は、単語同士に大小関係を導く
ウィンドウズ < マック < ユニックス
例えば「電機」という単語を索いてみる。 (辞書も大体 1000 ページ)
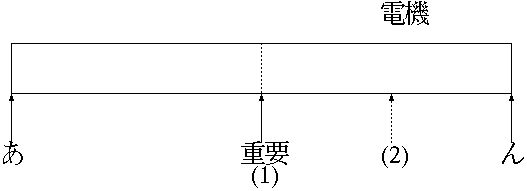
目的の単語を とする。 ある範囲( ページ目から ページ目) に目的の単語がある時、
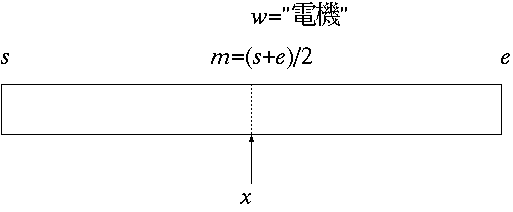
このような探索法を「二分探索法」と呼ぶ。
ページを開く回数はどれくらいか?
注目しているページは毎回半分ずつ減っていく。 全ページ数を N とする。
| 回数 | 注目しているページ数 | 注目しているページ数 |
|---|---|---|
より、 回となる。 1000ページの本だと、 回程度の検索で目的の単語を発見できる。
どんな問題でも考えれば解き方があるとは限らない!!!
プログラムを書くことができない問題を紹介する。
その前に……
速度や、効率や、手法などが異なるとしても、 コンピュータで yes, no を判別できることと、人間が yes, no を判別できることは 同じであると考えることにしよう。
これはチャーチが勝手に言ったことで、別に根拠も証明もないが、深く考えると、 それほど間違っているようには思えないと思う人は多い。
つまりこの章で紹介する「アルゴリズムの無い問題」は「人間も解くことができない問題」であると考える。
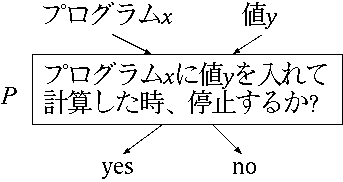
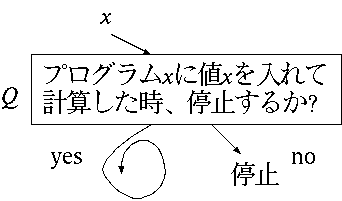
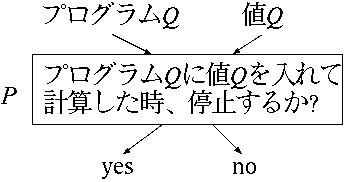
あらかじめコンピュータプログラムを読んで、そのプログラムが停止するか停止しないかを判断することはできない。これは理論的に証明されている。 これを「停止問題」といい、代表的な決定不能問題である。
したがって、どんなにコンピュータや科学が進歩しても、次のようなプログラム(ソフトウェア)は現れない。
但し、プログラムの書き方などを制限すると判断可能にすることもできる。
ポストの対応問題とは次のような問題である。
次のようなカードが何種類かあったとする。
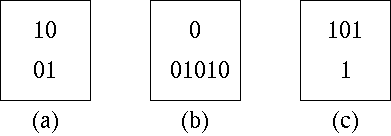
これらのカードを何枚も使用してよいという前提で、上下の記号の列が等しくなるようにできる組合せがあるかないかを判別する。
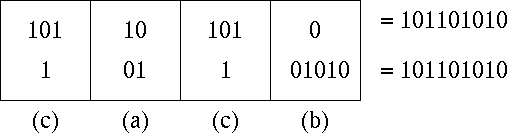
背理法と対角線論法により証明する。
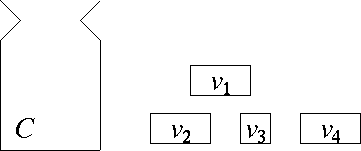
対角線論法の例
0 から 1 までの実数を数え上げることはできない。
数え上げられたとして、矛盾を導く。
各実数を無限小数で表すとする。 1 番目の実数の小数第一位を 、 2 番目の実数の小数第二位 を 、 3 番目の実数の小数第三位 を 、 …… とする。 とする。
さて、 小数第一位が , 小数第二位が , 小数第三位が , …… という数 を考える。 は 0 から 1 の間に入る数であるが、数え上げられていない。 実際、もし 番目に数え上げられていたと すると、小数第 位は でなければならない。 しかし、 の小数第 位は で、これは必ず と異なる。 したがって、実数を数え上げられたとする仮定に矛盾する。
1: 0.4124867591... 2: 0.8234971634... 3: 0.1498471681... … … 0.5704817516... (この証明は不完全である。 0.29999999 と 0.30000000 など同じ数で2種類の表示の 一方排除するような吟味が必要である。)
世の中には速いアルゴリズムがなさそうな問題がある。
これから紹介する問題は、一見単純で、検証も簡単ではあるが、速いアル ゴリズムが無さそうだと信じられている問題である。 もし、速いアルゴリズムを作ることができたら、画期的な大発見になる。
目的地が幾つかあり、目的地間の交通費がそれぞれ判っているとき、 全部の目的地に行くのに、かかる交通費が予算より多いか少いかを判断する問題。
荷物を選んで、ナップザックに丁度一杯になるように詰められるかどうかを判断する問題。
今紹介した問題は、「条件を満す特定の組合せかたがわかれば、その組合せで yes になることが容易にチェックできる」という構造を持つ。 このような問題は「NP完全問題」と呼ばれる。 (「NP完全問題」は数学的に厳密に定義されているが、ここでは省略する)
例えば、「囲碁は先手必勝か?」のような問題だと、必勝手順は相手 の手により様々に変化するので、短時間にはチェックできない。 つまり、正解を知っても効率良く検証できない。 したがって、このような「ゲームの必勝手順があるか無いか?」のような問題 は NP 完全問題より難しいと考えられる。
なお、囲碁では最終ポイント集計において、後手に6.5ポイント加算す ると経験的、統計的に互角になるとされ、一般の対局ではこのハンデが加算さ れる(コミ)。
なお、「オセロゲームが後手必勝か?」については、解明されたとの報告がある。