論理式の充足可能性問題(SAT: Satisfiability) とは与えられた 論理式を真にするような変数の割当が存在するかどうかを判定する問題です。 これは、変数の割当を非決定的に guess して、実際に論理式に代入して真か どうかを判定できますので、 NP に含まれる問題です。
これが NP 完全問題であることを示すには、NP に含まれるあらゆる問題が SAT に reducible であることを示さなければなりません。 そこで、 素朴な NP 完全問題である CNP を SAT に変換することを考えま す。 つまり、NP に含まれるある問題の入力 x が与えられた時、その問題を解く非 決定性の Turing 機械に入力 x を与えた状態を考えます。 そしてそれを非決定的に多項式時間実行した時 accept する計算が存在するか どうかを判定する問題を考え、これを論理式の充足可能性問題に置き換えます。
非決定性の多項式時間の計算を論理式の充足可能性に置き換えるには、様相の 列を考えます。 多項式時間の計算において、 1 step に必要な様相の長さは多項式で抑えられ ます(Ntime(p(N))⊆Nspace(p(N)))。この様相を多項式時間分だけ並べても、 合計で多項式程度の量で済みます。 一般性を失わず、Turing 機械のテープに書き込めるアルファベットを 0, 1 に制限できますが、これにより論理変数一つをテープのマスに対応させ、様相 を論理変数の列で表すことができます。 そして、次のような論理式を考えます。
(初期様相は与えられた入力 x がテープに書かれている) ∧ (各ステップ間の様相は、問題を解く非決定性 Turing 機械の動作に適合している) ∧ (最後の様相は受理様相である)
このような論理式を真にするには、最後が受理様相になるような、正しい様相 の列に対応した論理変数の割当が必要になります。 また入力 x がもともとの問題で yes になるときだけこのような割り当ては存 在します。 従って、このような構成を具体的に決定性多項式時間の手続きで示せれば、この 定理を証明できることになります。
ここで、時刻 t の j 番目のテープのマスに書かれている内容を tape(t,j) で表します。時刻 t の状態を state(t)、時刻 t のヘッドの位置を head(t) とします。state(t), head(t) はそれぞれ、論理変数の列になってます。 (state(t) は与えられた Turing 機械から決められる定数個、 head(t) は最 大計算時間の log 程度の長さ) f を最大計算時間 |x|c とします。
このようにすると、各時間に対して次の時間との全テープの関係を調べること になりますが、このようにしても多項式時間になります。 従って、論理式の充足可能性問題は NP 完全になります。
これを示すには、 SAT の入力(論理式) を巡回セールスマン問題の入力に変換できることを示し ます。
しかし、直接示すと煩瑣になるので、手順を分割します。 具体的には、 SAT を 3SATへ、 3SAT を有向ハミルトン閉路問題へ、有向ハミルトン閉路問 題を巡回セールスマン問題へ変換します。 つまり、 次を示します。
3SAT とは、特別な形のみを許した論理式に対する充足可能性問題です。 特殊な形とは、まず和積標準形という、変数の OR の式の集まりの積のみを許 し、さらに各 OR の式は変数が 3 つまでしか出てこないものを考えます。 和積標準形だけで全ての論理関数を表すことができます。 ここで、注意しなければならないので、前節で示した非決定性 Turing 機械を 表す論理式は和積標準形に簡単に直せるということです。 それは、(A ならば B) は (¬ A ∨ B) と直せ、また、複数の式を全て AND でつないでいるからです。 また、長さが 3 でない論理和の式は次のようにして直します。
どの書き換えも元の式の多項式程度の長さになりますので、 厳密な証明ではあ りませんが、 SAT ≦ 3SAT が示せたとします。
が充足可能なことと、 が充足可能なことが一致することを証明しなさい。
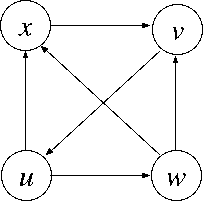
有向ハミルトン閉路問題とは、有向グラフで全ての頂点をちょうど一回だけ通って 出発点に戻ってくる閉路(ハミルトン閉路)が存在するかどうかと いう問題です。 次のような有向グラフが与えられた時、巡回セールスマン問題へ変換する方法 を説明します。 なお、下図では x→v→u→w→x というハミルトン閉路が存在します。

変換前の各頂点を変換後は辺で一直線につながった 3 つの頂点で表します。 例えば、頂点 x は x1, x2, x3 と 3 つの頂点になり、 x1 と x2, x2 と x3 は無向辺でつながっ ているとします。 そして、もともとあった有向辺は x から y への辺な ら、 x3 から y1 への無向辺とし ます。 上の有向グラフをこのように変換したのが次の図です。
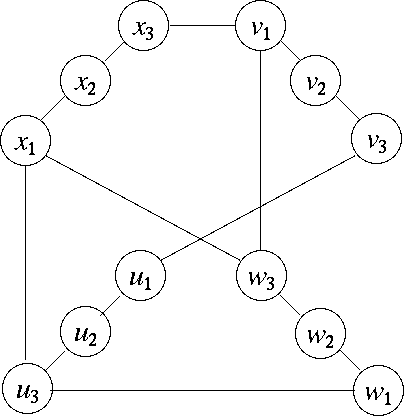
このグラフで辺の向きを無視して各頂点を一回だけ通って元に戻るような閉路 (ハミルトン閉路)の存在を考えると元の有向グラフのハミルトン閉路の存在と 一致します。 その理由を説明します。
x2を通過する時必ず x1, x2, x3 の順で通過しなければなりません。 変換後のグラフで x1 を通った時、次に x2 を通らないとハミルトン閉路になりません。 そこで、 x1 を通ったら、順に x2、 x3 を通る必要があり ます。 そして、x3 からは元の有向グラフにおいて x から出る辺のみが接続されています。 従って、もとの有向グラフの頂点の通り方と変換後の無向グラフの頂点の通り 方は対応しています。
さらに、この無向グラフで接続している頂点間のコストを 1、接続していない 頂点のコストを 2 とし、予算を全頂点数とすると巡回セールスマン問題とな り、全ての頂点をちょうど一回だけもとの無向グラフの辺上にたどれる時だけ 予算内に収まる巡回経路が存在します。 これらの変換は多項式時間で可能なため、有向ハミルトン閉路問題 ≦ 巡回セール スマン問題が示せたことになります。
これを示すには 3 変数ずつ含まれる和積標準形の論理式を有向グラフに変換 する必要があります。 これにはまず次の交差グラフを考えます。
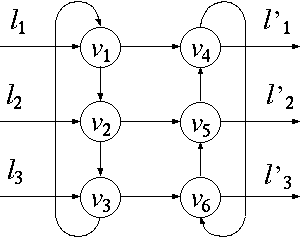
交差グラフは入力線 l1 l2 l3 と出力線 l'1 l'2 l'3 を持ちます。 そして、入力線を 1, 2, 3 本のいずれかを選ぶと、全ての頂点を通る通り方 が一意に決まるという性質があります。 例えば、 l1 一本のみ選ぶと、 v3 を通過するために v2 v3 と通る必要があります。 そして、 v3から v6 を通る ためには v5、 v6 の順に通る必要が あります。この時必ず l ' 1 の線を通ることになり ます。
さらに、 l1、 l1の 二本を選ぶと、 v3 を通過するには v2 から v3へ通る必要があ ります。 そして、 v3 からは v4 へ しか出られません。 そして、 v5 には、 v4 からしか通過できず、 v1 からはたどり着けません。 従って、 l1 からは l ' 1 へ、 l2 からは l ' 2 へ通 ることになります。 3 本選んだ時は、真横に通過しないと全ての頂点を一回だけ通過することが できなくなります。
このような交差グラフ一つを、論理式の和の一つと関連づけます。 以後、簡単のために、論理式を一つ与えられた時、それをどのように有向グラ フに変換するかを例を使って説明します。 与えられた論理式を とします。 この式を有向グラフに変換します。 ∧で繋げられた節は 3 つありますので、交差グラフを 3 つ使います。 その他に変数を表す頂点を 3 + 1 個用意します。 変数を表す頂点からは と を表す二つの有向辺が出ます。 そして、その変数を使用している節の入力辺の一本に接続し、出力辺を次の入 力辺へ接続します。そして、最後に次の頂点へ接続します。
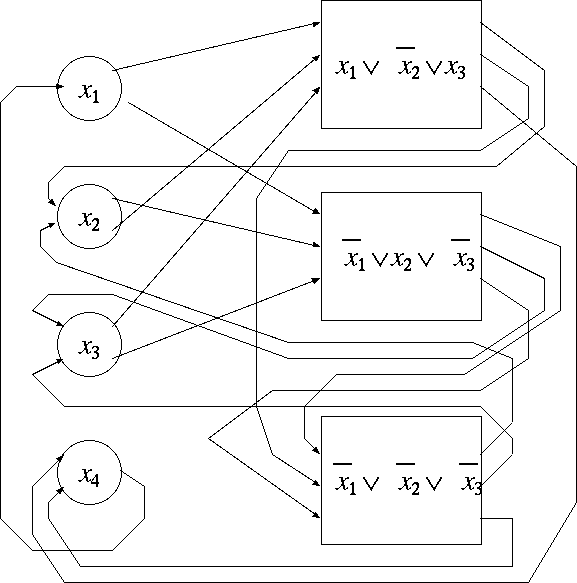
このようにすると、最終的に頂点辺からは と のどちらかを選ぶことになりますが、これはそ の値が真になることを意味します。 そして、そこから出る辺が入る交差グラフの頂点は全部通過することになりま すので、元の論理式の充足可能性と、このグラフのハミルトン閉路の存在性が 一致します。 またこの変換は多項式時間で可能です。 以上により 3SAT ≦ 有向ハミルトン閉路問題 が示せたことになります。